Sul numero 11 (Aprile 1981) della
rivista Micro e Personal Computer, alla quale ero all'epoca
abbonato, apparve una prova della scheda a microprocessore Amico 2000 ma
la parte che più mi interessò era un piccolo trafiletto (vedi sotto)
all'interno dell'articolo nel quale si parlava della risoluzione di un giochino (non identificato)
usando appunto il predetto Amico 2000 con un metodo metà a tentativi e
metà analitico che comunque aveva portato alla soluzione del quesito.

Perché allora non tentare di
risolverlo con la mia TI-59? Dopo qualche settimana di tentativi
analitici (provando a risolvere in qualche maniera il sistema che
risultava di 15 equazioni in 19 incognite) avevo dato forfait e
"seppellita" l'intera faccenda. Qualche settimana fa, sistemando delle
vecchie carte, ho trovato le mie note dell'epoca ed ho deciso di riprendere in
mano la questione anche approfittando del fatto che oggi l'hardware (ed
il software) a disposizione è ben più capace.
Così identificato il nome del
giochino(!) e cioè l'"Esagono Magico" mi sono documentato su Internet ed
ho trovato un po' di materiale, ma pochissimo software (tantomeno per la
59) e così mi sono deciso a scrivere un programma usando il solito Quick
Basic. Il risultato finale dopo cinque o sei scritture è stato
HEXAGON.BAS che compilato ed eseguito su un CoreDuo in circa 15
secondi trova tutte le 12 soluzioni. Così per sfizio ho riscritto il
codice in C - compilandolo usando sia il Turbo C 2.01 della
Borland che il Quick C 2.0 della Microsoft -, in Pascal - con il Quick
Pascal della Microsoft -, in Fortran - 77 per PC IBM - ed anche in linguaggio ERRE (vedi la pagina su
ERRE PROJECT).
A questo punto è iniziata la
traduzione in SOA per poterlo far girare sulla TI-59: dopo qualche
studio teorico per poter ridurre il numero delle variabili coinvolte e
limitare gli estremi sulle altre il risultato finale è stato il
programma HEXAGON4.SOA di 322 passi che ha prodotto (sul
mio emulatore di TI-59) la prima soluzione dopo
circa 20 minuti (grosso modo un giorno di elaborazione sulla TI-59
reale e probabilmente una decina di giorni per tutte le soluzioni). Visti gli spazi occupati l'ho anche adattato
per le TI-58/58C ed
ecco
HEXAGON3.SOA (che produce gli stessi risultati del suo fratellino)
di 309 passi e che gira usando la partizione 2 Op 17
→ 319.19 (!).
Le variabili utilizzate dal programma Basic sono
numerate da A1 ad A19 e sono così disposte:
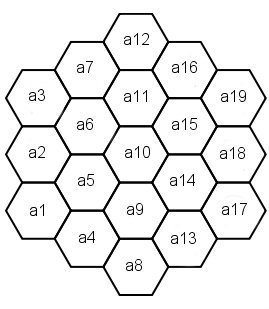
Nella traduzione è stato rispettato
quest'ordine così A1 diventa R01, A2 R02 e così via.
Le prime cinque soluzioni prodotte
dai due programmi HEXAGON sono le seguenti:
|
3. 01
17. 02
18. 03
19. 04
7. 05
1. 06
11. 07
16. 08
2. 09
5. 10
6. 11
9. 12
12. 13
4. 14
8. 15
14. 16
10. 17
13. 18
15. 19
0. 20
0. 21
42504. 22
0. 23
0. 24
0. 25
0. 26
0. 27
0. 28
0. 29 |
9. 01
11. 02
18. 03
14. 04
6. 05
1. 06
17. 07
15. 08
8. 09
5. 10
7. 11
3. 12
13. 13
4. 14
2. 15
19. 16
10. 17
12. 18
16. 19
0. 20
0. 21
65080. 22
0. 23
0. 24
0. 25
0. 26
0. 27
0. 28
0. 29 |
3. 01
19. 02
16. 03
17. 04
7. 05
2. 06
12. 07
18. 08
1. 09
5. 10
4. 11
10. 12
11. 13
6. 14
8. 15
13. 16
9. 17
14. 18
15. 19
0. 20
0. 21
533063. 22
0. 23
0. 24
0. 25
0. 26
0. 27
0. 28
0. 29 |
10. 01
12. 02
16. 03
13. 04
4. 05
2. 06
19. 07
15. 08
8. 09
5. 10
7. 11
3. 12
14. 13
6. 14
1. 15
17. 16
9. 17
11. 18
18. 19
0. 20
0. 21
589439. 22
0. 23
0. 24
0. 25
0. 26
0. 27
0. 28
0. 29 |
9. 01
14. 02
15. 03
11. 04
6. 05
8. 06
13. 07
18. 08
1. 09
5. 10
4. 11
10. 12
17. 13
7. 14
2. 15
12. 16
3. 17
19. 18
16. 19
0. 20
0. 21
795633. 22
0. 23
0. 24
0. 25
0. 26
0. 27
0. 28
0. 29 |
Il registro R22 contiene il numero dei cicli effettuati fino a quel
momento: la prima soluzione arriva dopo 42504 cicli, il che spiega la lentezza
sulla TI-59 reale. Nella tabella sotto ho riportato, affiancati, i due
programmi: come si può vedere la traduzione è estremamente lineare. Da
notare che la versione SOA non ha bisogno dell'array VETT(.) del BASIC
in quanto i registri della TI-59 sono richiamabili sia direttamente che
indirettamente (tramite un indice).
HEXAGON.BAS
HEXAGON4.SOA
DEFINT A-Z
CLS : DIM vett(1 TO 19)
PRINT TIME$
a10=5
FOR a3 = 18 TO 3 STEP -1 '18
FOR a8 = 18 TO 3 STEP -1'15
FOR a12 = 18 TO 3 STEP -1 '3
FOR a17 = 18 TO 3 STEP -1 '10
FOR a15 = 8 TO 1 STEP -1 '2
FOR a6 = 8 TO 1 STEP -1'1
count# = count# + 1
a14 = 38 - a3 - a6 - a10 - a17
a13 = 38 - a8 - a17
a7 = 38 - a3 - a12
a16 = 38 - a13 - a14 - a15
a19 = 38 - a12 - a16
a18 = 38 - a17 - a19
a11 = 38 - a7 - a15 - a18
a9 = 38 - a8 - a10 - a11 - a12
a4 = 38 - a9 - a14 - a18
a1 = 38 - a4 - a8
a2 = 38 - a1 - a3
a5 = 38 - a4 - a6 - a7
'--------------- eq. non utilizzate ------
'a2 + a5 + a9 + a13 = 38
'a2 + a6 + a11 + a16 = 38
'a1 + a5 + a10 + a15 + a19 = 38
'-----------------------------------------
GOSUB VerificaSeUguali: IF NOT IsEqual THEN PRINT a1; a2; a3;
a4; a5; a6; a7; a8; a9; a10; a11; a12; a13; a14; a15; a16; a17;
a18; a19; ":"; count#
NEXT a6
NEXT a15
NEXT a17
NEXT a12
NEXT a8
NEXT a3
PRINT TIME$
END
VerificaSeUguali:
vett(1) = a1: vett(2) = a2: vett(3) = a3: vett(4) = a4: vett(5)
= a5: vett(6) = a6
vett(7) = a7: vett(8) = a8: vett(9) = a9: vett(10) = a10: vett(11)
= a11: vett(12) = a12
vett(13) = a13: vett(14) = a14: vett(15) = a15: vett(16) = a16:
vett(17) = a17: vett(18) = a18
vett(19) = a19
IsEqual = 0
IF ABS(vett(19) - 19) >= 19 THEN IsEqual = -1: RETURN
FOR i = 18 TO 1 STEP -1
IF ABS(vett(i) - 19) >= 19 THEN IsEqual = -1: EXIT FOR
FOR j = 19 TO i + 1 STEP -1
IF vett(i) = vett(j) THEN IsEqual = -1: i = 1: j = 1
NEXT j
NEXT i
RETURN |
{
Risolve l'esagono magico - tradotto da HEXFORTI.BAS
}
{ E' il più veloce in assoluto e il primo che gira in tempi}
{ decenti anche sulla TI-59 reale
}
{ Trova la prima soluzione dopo 42.504 cicli di calcolo
}
{ La SUB Basic VerificaSeUguali viene messa all'inizio per }
{
ottimizzare la velocità di esecuzione}
INV STF 01
RCL 19 X:T 0 GE SUM 2 0 X:T GE SUM
1 8 STO 21
LBL STO
RC* 21 X:T 0 GE SUM 2 0 X:T GE SUM
1 9 STO 00
LBL RCL
RC* 21 X:T RC* 00 EQ SUM
OP 30 1 + RCL 21 = X:T RCL 00 GE RCL
DSZ 21 STO RTN
LBL SUM
STF 01
RTN
{inizio esecuzione}
LBL A CMS 5 STO 10 { fissa il centrale a10}
1 8 STO 03
LBL CLR
1 8 STO 08
LBL CE
1 8 STO 12
LBL INV
1 8 STO 17
LBL SQR
8 STO 15
LBL X^2
8 STO 06
LBL 1/X
{ visualizza il ciclo attuale - R22 e' la variabile count#}
1 SUM 22 {RCL 22 PAU}
3 8 - RCL 03 - RCL 06 - RCL 10 - RCL 17 = STO 14
3 8 - RCL 08 - RCL 17 = STO 13
3 8 - RCL 03 - RCL 12 = STO 7
3 8 - RCL 13 - RCL 14 - RCL 15 = STO 16
3 8 - RCL 12 - RCL 16 = STO 19
3 8 - RCL 17 - RCL 19 = STO 18
3 8 - RCL 07 - RCL 15 - RCL 18 = STO 11
3 8 - RCL 08 - RCL 10 - RCL 11 - RCL 12 = STO 09
3 8 - RCL 09 - RCL 14 - RCL 18 = STO 04
3 8 - RCL 04 - RCL 08 = STO 01
3 8 - RCL 01 - RCL 03 = STO 02
3 8 - RCL 04 - RCL 06 - RCL 07 = STO 05
SBR 00 00 IFF 01 +/-
{stampa le soluzioni}
1 INV LST ADV
LBL +/-
DSZ 06 1/X
DSZ 15 X^2
1 INV SUM 17 3 X:T RCL 17 GE SQR {DSZ 17 SQR}
1 INV SUM 12 3 X:T RCL 12 GE INV {DSZ 12 INV}
OP 38 3 X:T RCL 08 GE CE {DSZ 08 CE }
OP 33 3 X:T RCL 03 GE CLR {DSZ 03 CLR}
R/S
|
La faccenda sembrava finita qui, ma
mi ha "disturbato" la lentezza dell'esecuzione della versione SOA, così
ho esaminato più attentamente il programma SUMSUP.C
(il più adatto dei due prelevati da Internet)
che risolve il problema in modo più elegante del mio ed anche più
veloce; l'unico rischio era che la traduzione fosse troppo complicata ed
andasse oltre le capacità della 59. Così dopo averlo riscritto senza
usare le strutture #define dell'originale che lo rendevano più leggibile,
ma anche difficilmente traducibile in altri linguaggi, l'ho codificato
anche in Pascal, in Quick Basic, in Fortran 77 ed anche in
ERRE. Comunque i tempi di esecuzioni
della versione in C sono mostruosi: in meno di un secondo vengono
stampate tutte le soluzioni !
Proprio ERRE mi ha facilitato molto
il compito perché il suo compilatore (che in realtà è un cross-compiler)
produce un programma Basic con tutti i salti esplicitati e perciò era
perfetto per la traduzione in SOA.
Il risultato finale è stato
SUMSUP2R.SOA (solo per la TI-59) in 540 passi (e quindi
partizione 559.49) che è anche molto veloce: con l'emulatore che gira
sul solito CoreDuo in neanche 40 minuti sono state stampate tutte le
soluzioni. Per l'esecuzione basta premere A. Adesso non resta che farlo girare sulla TI reale ......
* 000 76 LBL
001 18 C'
002 53 (
003 24 CE
004 85 +
005 03 3
006 00 0
007 54 )
008 42 STO
009 00 00
010 92 RTN
* 011 76 LBL
012 19 D'
013 18 C'
014 01 1
015 32 X:T
016 73 RC*
017 00 00
018 92 RTN
* 019 76 LBL
020 10 E'
021 42 STO
022 26 26
023 22 INV
024 86 STF
025 01 01
026 43 RCL
027 26 26
028 32 X:T
029 00 0
030 77 GE
031 96 WRT
032 02 2
033 00 0
034 32 X:T
035 77 GE
036 96 WRT
037 01 1
038 32 X:T
039 43 RCL
040 26 26
041 18 C'
042 73 RC*
043 00 00
044 67 EQ
045 96 WRT
046 86 STF
047 01 01
* 048 76 LBL
049 96 WRT
050 92 RTN
* 051 76 LBL
052 17 B'
053
18 C'
054 01 1
055 74 SM*
056 00 00
057 92 RTN
* 058 76 LBL
059 16 A'
060 18 C'
061 01 1
062 22 INV
063 74 SM*
064 00 00
065 92 RTN
* 066 76 LBL
067 11 A
068 47 CMS
069 01 1
070 09 9
071 42 STO
072 01 01
* 073 76 LBL
074 22 INV
075 43 RCL
076 01 01
077 19 D'
078 67 EQ
079 94 +/-
080 01 1
081 74 SM*
082 00 00
083 01 1
084 09 9
085 42 STO
086 03 03
* 087 76 LBL
088 24 CE
089 43 RCL
090 03 03
091 19 D'
092 67 EQ
093 95 =
094 01 1
095 74 SM*
096 00 00
097 03 3
098 08 8
099 75 -
100 43 RCL
101 01 01
102 75 -
103 43 RCL
104 03 03
105 95 =
106 42 STO
107 02 02
108 10 E'
109 22 INV
110 87 IFF
111 01 01
112 85 +
113 43 RCL
114 02 02
115 17 B'
116 01 1
117 09 9
118 42 STO
119 12 12
* 120 76 LBL
121 25 CLR
122 43 RCL
123 12 12
124 19 D'
125 67 EQ
126 75 -
127 01 1
128 74 SM*
129 00 00
130 03 3
131 08 8
132 75 -
133 43 RCL
134 03 03
135 75 -
136 43 RCL
137 12 12
138 95 =
139 42 STO
140 07 07
141 10 E'
142 22 INV
143 87 IFF
144 01 01
145 65 x
146 43 RCL
147 07 07
148 17 B'
149 01 1
150 09 9
151 42 STO
152 19 19
* 153 76 LBL
154 23 LNX
155 43 RCL
156 19 19
157 19 D'
158 67 EQ
159 55 :
160 01 1
161 74 SM*
162 00 00
163 03 3
164 08 8
165 75 -
166 43 RCL
167 12 12
168 75 -
169 43 RCL
170 19 19
171 95 =
172 42 STO
173 16 16
174 10 E'
175 22 INV
176 87 IFF
177 01 01
178 89 п
179 43 RCL |
180 16 16
181 17 B'
182 01 1
183 09 9
184 42 STO
185 17 17
* 186 76 LBL
187 33 X2
188 43 RCL
189 17 17
190 19 D'
191 67 EQ
192 53 (
193 01 1
194 74 SM*
195 00 00
196 03 3
197 08 8
198 75 -
199 43 RCL
200 19 19
201 75 -
202 43 RCL
203 17 17
204 95 =
205 42 STO
206 18 18
207 10 E'
208 22 INV
209 87 IFF
210 01 01
211 52 EE
212 43 RCL
213 18 18
214 17 B'
215 01 1
216 09 9
217 42 STO
218 08 08
* 219 76 LBL
220 34 √X
221 43 RCL
222 08 08
223 19 D'
224 67 EQ
225 54 )
226 01 1
227 74 SM*
228 00 00
229 03 3
230 08 8
231 75 -
232 43 RCL
233 17 17
234 75 -
235 43 RCL
236 08 08
237 95 =
238 42 STO
239 13 13
240 10 E'
241 22 INV
242 87 IFF
243 01 01
244 57 ENG
245 43 RCL
246 13 13
247 17 B'
248 03 3
249 08 8
250 75 -
251 43 RCL
252 01 01
253 75 -
254 43 RCL
255 08 08
256 95 =
257 42 STO
258 04 04
259 10 E'
260 22 INV
261 87 IFF
262 01 01
263 58 FIX
264 43 RCL
265 04 04
266 17 B'
267 01 1
268 09 9
269 42 STO
270 05 05
* 271 76 LBL
272 35 1/X
273 43 RCL
274 05 05
275 19 D'
276 67 EQ
277 59 INT
278 01 1
279 74 SM*
280 00 00
281 03 3
282 08 8
283 75 -
284 43 RCL
285 04 04
286 75 -
287 43 RCL
288 05 05
289 75 -
290 43 RCL
291 07 07
292 95 =
293 42 STO
294 06 06
295 10 E'
296 22 INV
297 87 IFF
298 01 01
299 50 |X|
300 43 RCL
301 06 06
302 17 B'
303 03 3
304 08 8
305 75 -
306 43 RCL
307 02 02
308 75 -
309 43 RCL
310 06 06
311 75 -
312 43 RCL
313 16 16
314 95 =
315 42 STO
316 11 11
317 10 E'
318 22 INV
319 87 IFF
320 01 01
321 66 PAU
322 43 RCL
323 11 11
324 17 B'
325 03 3
326 08 8
327 75 -
328 43 RCL
329 07 07
330 75 -
331 43 RCL
332 11 11
333 75 -
334 43 RCL
335 18 18
336 95 =
337 42 STO
338 15 15
339 10 E'
340 22 INV
341 87 IFF
342 01 01
343 81 RST
344 43 RCL
345 15 15
346 17 B'
347 03 3
348 08 8
349 75 -
350 43 RCL
351 13 13
352 75 -
353 43 RCL
354 15 15
355 75 -
356 43 RCL
357 16 16
358 95 =
359 42 STO |
360 14 14
361 10 E'
362 22 INV
363 87 IFF
364 01 01
365 61 GTO
366 43 RCL
367 14 14
368 17 B'
369 03 3
370 08 8
371 75 -
372 43 RCL
373 04 04
374 75 -
375 43 RCL
376 14 14
377 75 -
378 43 RCL
379 18 18
380 95 =
381 42 STO
382 09 09
383 10 E'
384 22 INV
385 87 IFF
386 01 01
387 71 SBR
388 43 RCL
389 09 09
390 17 B'
391 03 3
392 08 8
393 75 -
394 43 RCL
395 01 01
396 75 -
397 43 RCL
398 05 05
399 75 -
400 43 RCL
401 15 15
402 75 -
403 43 RCL
404 19 19
405 95 =
406 42 STO
407 10 10
408 10 E'
409 22 INV
410 87 IFF
411 01 01
412 68 NOP
413 43 RCL
414 10 10
415 17 B'
416 01 1
417 22 INV
418 90 LST
419 98 ADV
420 43 RCL
421 10 10
422 16 A'
* 423 76 LBL
424 68 NOP
425 43 RCL
426 09 09
427 16 A'
* 428 76 LBL
429 71 SBR
430 43 RCL
431 14 14
432 16 A'
* 433 76 LBL
434 61 GTO
435 43 RCL
436 15 15
437 16 A'
* 438 76 LBL
439 81 RST
440 43 RCL
441 11 11
442 16 A'
* 443 76 LBL
444 66 PAU
445 43 RCL
446 06 06
447 16 A'
* 448 76 LBL
449 50 |X|
450 43 RCL
451 05 05
452 16 A'
* 453 76 LBL
454 59 INT
455 97 DSZ
456 05 05
457 35 1/X
458 43 RCL
459 04 04
460 16 A'
* 461 76 LBL
462 58 FIX
463 43 RCL
464 13 13
465 16 A'
* 466 76 LBL
467 57 ENG
468 43 RCL
469 08 08
470 16 A'
* 471 76 LBL
472 54 )
473 97 DSZ
474 08 08
475 34 √X
476 43 RCL
477 18 18
478 16 A'
* 479 76 LBL
480 52 EE
481 43 RCL
482 17 17
483 16 A'
* 484 76 LBL
485 53 (
486 97 DSZ
487 17 17
488 33 X2
489 43 RCL
490 16 16
491 16 A'
* 492 76 LBL
493 89 п
494 43 RCL
495 19 19
496 16 A'
* 497 76 LBL
498 55 :
499 97 DSZ
500 19 19
501 23 LNX
502 43 RCL
503 07 07
504 16 A'
* 505 76 LBL
506 65 x
507 43 RCL
508 12 12
509 16 A'
* 510 76 LBL
511 75 -
512 97 DSZ
513 12 12
514
25 CLR
515 43 RCL
516 02 02
517 16 A'
* 518 76 LBL
519 85 +
520 43 RCL
521 03 03
522 16 A'
* 523 76 LBL
524 95 =
525 97 DSZ
526 03 03
527 24 CE
528 43 RCL
529 01 01
530 16 A'
* 531 76 LBL
532 94 +/-
533 97 DSZ
534 01 01
535 22 INV
536 91 R/S
* 537 76 LBL
538 99 PRT
539 92 RTN |
|




